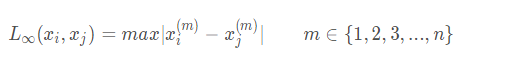通常，数据集可以看作数据对象的集合。数据对象有时也叫做记录、点、向量、模式、事件、案例、样本、观测或实体。数据对象用一组刻画对象基本特性(如物体质量或事件发生时间)的描述。属性有时也叫做变量、特性、字段、特征或维。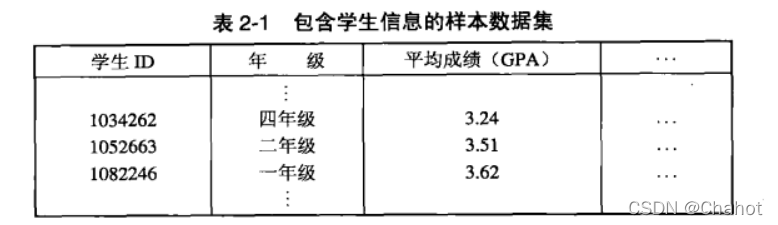 
数据集是一个文件，可以用表格来表示。其中每一行表示一个数据对象，而每一列表示一个特有的属性。这是关系型数据库中的典型表现，但是由于还存在其他类型的数据库，因此这样的定义也不是绝对的。但是作为对数据的属性和对象的浅层理解，在这个位置这样的解释个人认为是合理的。
属性（attribute）就是对象的性质或者特性，因对象而已，也可以随某变量而变化。如时间。 属性分为符号属性和数值属性，其中数值属性的可以取无限个不同值的，但是符号属性有一个固定的值域，它只有有限的种类。 测量标度（measurement scale）：将数值或符号与对象属性关联的规则。 任何时候我们都在进行这样的测量过程，比如将人分为男女的分类法，比如清点某物品数目确保足够使用的对比法。这种规则多种多样且一直存在。
用于代表属性的值可能具有不同于属性的性质，属性的性质可以与值无关。如学号、ID这种数字串，或者年龄。这些属性的值在某些情况下是有意义的，如讨论平均年龄，但是讨论平均学号却毫无意义。对学号这种属性，判断他们价值的标度是对比是否一致，如果一致则判定为归属于某个体。 
以上是属性的不同类型，或者说不同性质。分别是相异性、顺序性、可加、可乘性。对应这四种属性，我们也定义了四种类型，分别是标称Nominal，序数Ordinal，区间Interval，比率Ratio。具有向上兼容性，即满足比率的属性，其一定满足其他三种要求，而满足标称的属性，未必满足其他三种类型的性质。 
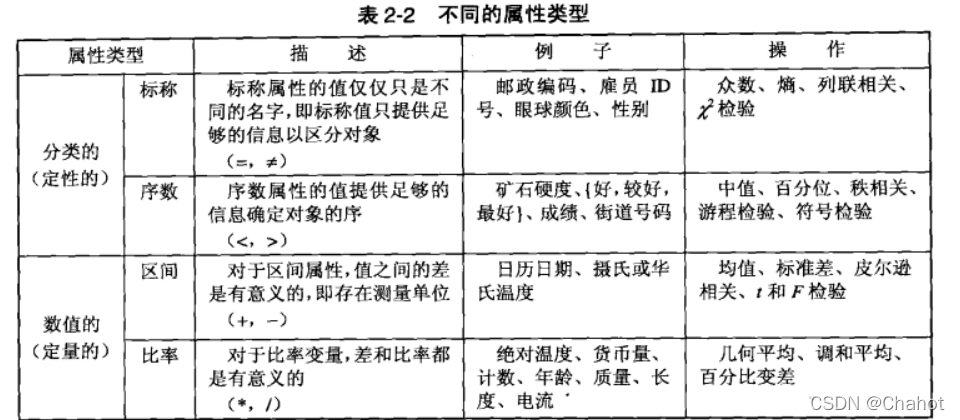标称和序数属性统称分类的(categorical) 或定性的(qualitative) 属性。顾名思义，定性属性(如雇员ID)不具有数的大部分性质。即便使用数(即整数)表示，也应当像对待符号- -样 对待它们。其余两种类型的属性,即区间和比率属性,统称定量的(quantitative )或数值的( numeric)属性。定量属性用数表示，并且具有数的大部分性质。注意:定量属性可以是整数值或连续值。 属性的类型也可以用不改变属性意义的变换来描述。用允许的变换(permissible transformation)定义了表2-2所示的属性类型。例如，如果长度分别用米和英尺度量，其属性的意义并未改变。 
当我们用不同单位测量相同的对照组，结果是不同的，但是它们表达的意义是相同的。对于长度，结果始终是一个比一个长，实际数值的改变不能改变意义上的象征作用。 再比如：温度标度。有华氏度和摄氏度，其中2摄氏度是1摄氏度的两倍，但是用华氏度表示的时候却不满足这个倍数关系。因此对于温度这个属性，华氏度和摄氏度的比率并没有意义。
连续性也可以说是可能取值的个数。 
离散的属性：数值的个数即有限。这样的数值是可分类的，计算机科学中一般用二元属性（binary attribute）是最常用的，这是一种离散的只接受两个值的情况。用0-1表示。 连续的属性：是实数值，如温度高度重量等。可以使用连续的浮点数表示，实践过程中，实数值只能表示有限精度的测量标度。 这里提一下非对称属性，细节会在将来的博文中出一篇详细的。大体说一下概念，就是当我们统计一个二元属性的时候，如选课情况，一个学校几千名学生，它们选择某一个课的学生的最大数额就是几十名。则如果用1表示选课，0表示没有选择该课程，就会发现从数据整体而言，绝大多数数据都是0，只有极小一部分是1，这从存储、实际应用等多种角度分析而言都不利，因此我们不想使用这种抵消的分类方法。只有非零值才重要的二元属性是非对称的二元属性。
首先是数据集的特性： 维度（dimensionality）：简单而言就是属性的数目。高纬度数据与低纬度数据的处理时有着本质的不同。分析高纬数据可能会陷入维灾难（curse of dimensionality）。数据处理一般要先降维再处理。降维的操作被称为【维归约】（dimensionality reduction） 稀疏性（sparsity）：可能某些数据集的大部分属性的值都是0，非零项非常少，这种时候我们只需要筛选非零项；可以大量节约存储空间和计算时间 分辨率（resolution）：常常可在不同分辨率下得到数据，而且性质不同。简单来说当我们使用卫星观察地球，和肉眼观察地球，一个波澜壮阔一个就是一个平面图。分辨率太高太低都会损失一些属性，所以要选择适合的分辨率。如肉眼去观察气象变化则毫无意义，卫星去观察蚂蚁窝的分布同理。
数据记录（record）
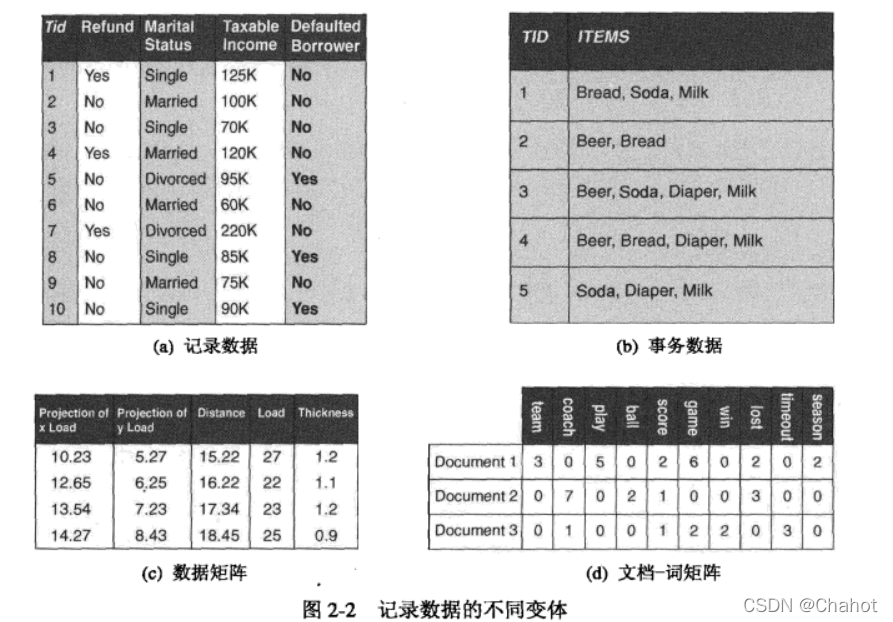事务数据：transaction：一种特殊的记录数据，每个事务设计一系列的项。这种数据的类型被称为购物篮数据（market basket data）。一般而言象征某个事务具有哪些属性，这些属性用二元属性表示有误，如商品是否已购买，则未购买的属性不需要列入这个购物篮内。这些属性可以是离散或连续的，比如购买商品的数量和开销。 数据矩阵：如果一个数据集中的所有数据对象都有相同的属性集，则数据对象有看为空间中的向量，每个维度代表一个不同属性，就可以使用一个m x n的矩阵表示。这种数据矩阵的标准运算操作可以对数据进行标准处理。
稀疏矩阵：只有非零值才有意义的矩阵，如图2-2d
图（graph）
图形更直观有效的表示了数据间的关系，也可能表示数据的本身。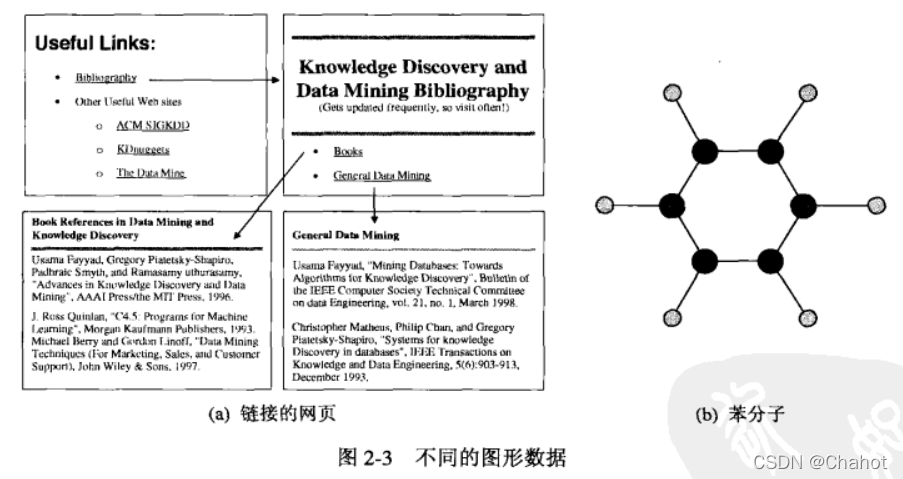 
表示关系这一点很好理解，可能是先后的承接关系也可能是物理位置上的连接关系（等等）。具有图形对象的数据是指如果对象具有结构，如原子、分子、化学键等，则图本身就具有意义。
有序数据（Orderd）
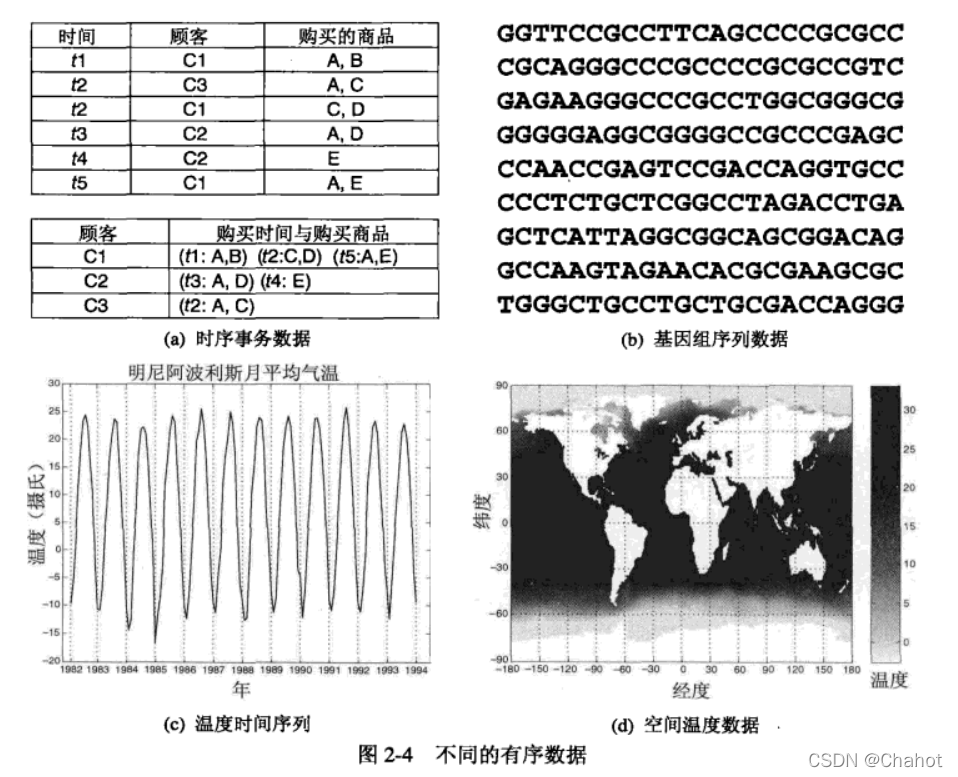更好理解，如图所示。元素的位置如果改变，则本身的意义也会改变。 时序数据：sequential data：也成为时间数据temporal data。可以看做记录数据的扩充，每个记录包含一个相关联的时间。2-4a表示不同时间段不同客户购买的商品。 序列数据：sequence data：是一个数据集合，是各个实体的序列，如词或者字母的序列。 时间序列数据：time series data。是一种特殊的时序数据，每个记录都是一个时间序列，是一段时间以来的测量序列。2-4c表示几年来的月平均气温的变化。 空间数据：对象具有位置或者区域属性。空间数据的一个例子是从不同的地理位置收集的气象数据。 时间序列数据和空间数据都有一个自相关属性，即时间或者空间距离近的时候，其各属性也十分相似。
数据挖掘使用的数据都是原始数据，这些数据有很多难以操作和处理，不能直接使用。统计学中使用的大部分数据是已经处理好的高质量数据，但是实际上从源头控制数据质量是不可能的，因此数据挖掘的第一步就是将数据的质量提高，方法大概有两种，一个是想办法提高数据质量，一个是使用可以容忍一定程度低质量的算法来进行数据处理。 测量误差（measurement error)：测量数据过程中出现的问题，如，数据是连续的，那么在精确的测量工具测量出来的实际数值也有一定的偏差。这种偏差是由精确度导致的误差。 数据收集错误（data collection error）：如遗漏某对象的属性值，不当包含了不属于对象的属性值等。 以上两种错误可能是系统不可避免的，也可能是失误导致的。医学制药时，我们会首先在小鼠身上做实验，取得成果后会逐步推荐到人体实验。实际上步骤再怎么完美，两种物种具有太多的潜在属性，因此对小鼠的实验过渡到人体实验之前，具有很大一部分的系统误差，这并不是专家低估了变量，而是难免会存在的区别。 噪声：测量误差的随机部分。属于系统误差。噪声通常包含时间和空间向量，完全消除噪音是很困难的，但是数据挖掘关注的鲁邦算法robust algorithm是一种能够在一定忍受范围内的噪音干扰下获得满意结果的解决方法。 伪像artifact：数据错误可能是更确定现象的结果，如程序bug导致的数据错误，如一组照片上每个相同位置都出现了裂痕，这些是有固定的原因导致的，这种失真被称为伪像。 精度（precision）：重复测量值之间的接近程度 偏倚（bias）：测量值与被测量值之间的系统的变差。精度通常 例题如下： 
准确率：是一个依赖于精度和偏倚的衡量标准，是一个一般化的概念，因此没有用这两个量表达的一般化公式。
离群点outlier：异常数据，即大部分数据表现某一特征的时候，突然某个数据表现了一个完全不同或者差距极大的特征。也被称为异常对象或者异常值（anomalous）。 遗漏值：数据收集不全的情况会因为各种原因发生。发生这种情况时，我们可以选择删除这个遗漏的对象（最简单有效，虽然会导致数据不完整，但是如果遗漏值过多反而可能会给数据分析结果带来更大的误差）；估计遗漏值（但是要可靠的）；分析时忽略遗漏值（在分析结果出来后计算各种数式时，删除掉遗漏值的占比）等。 重复的数据根据需求要降重，没有必要的重复数据删除，仅保留数据库的属性度量上相同但是代表的是不同对象的属性。
对收集到的低质量数据，我们需要进行处理才能更便于我们进行分析。因此需要的步骤如下： 
聚集，抽样，降归约，特征子集选择，特征创建，离散化和二元化，变量变换。 其中特征或变量可以替换属性这个术语。
聚集： 将两个或多个对象合并成单个对象。如把一天内的所有客户购物的事务整理成日购买信息表这一过程。合并过程中存在一些难点，如怎么合并属性的值，像价格这类的我们可以用平均值或求和来处理，不同的属性有不同的要求。一个聚合的属性集中每个属性都是一个维，这样的聚集通常用OLAP联机分析处理来聚类，这会单独出一篇博文说明OLAP。 聚集的动机有很多，包括减少内存和处理时间，方便计算等多种情况。 抽样：有效抽样要抽取有代表性的样品。它近似的与具有与原数据集相同的性质。有很多抽样方式。 单随机抽样（simple random sampling）：分为无放回和有放回。选取任何特定项目的概率是相等的。 分层抽样（stratified sampling）：从预先制定的组开始抽样，尽管每组的大小不同但是抽取的对象个数相同。用于抽取注重与比率、频率的稀有样品时的操作。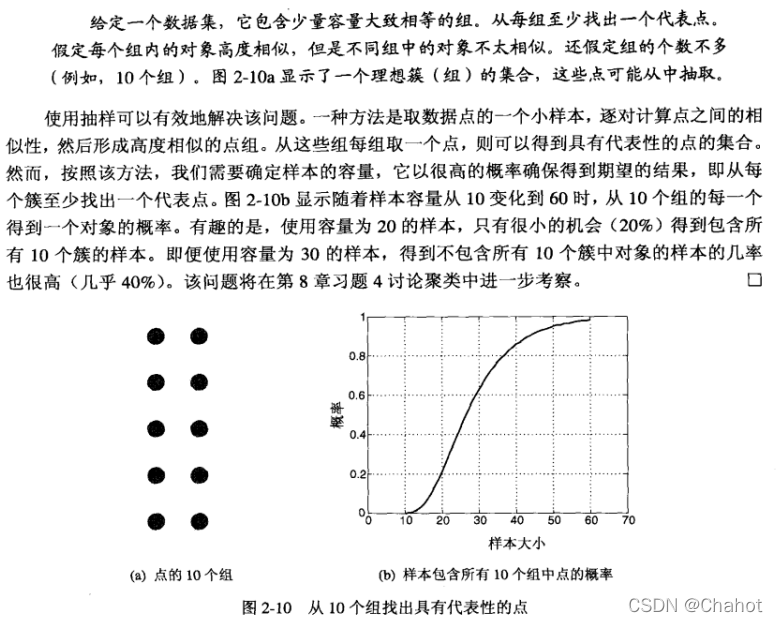 
渐进抽样和自适应【progressive sampling】【adaptive】：这些方法从一个小样本开始，然后逐渐增加样本容量到获得一个大样本。需要一种评估样本体积的方法来估计出稳定点的接近程度从而停止抽样。
维归约：降维可以更好的方便数据挖掘算法的处理。主要方法是使用线性代数技术，将数据从高维空间投影到低纬空间，特别是对于连续数据。Principal Componets Analysis【PCA】主成分分析是一种用于连续属性的线性代数技术，代表方法有SVD奇异值分解。 特征子集选择：不同的相关特征可能对不同的数据挖掘任务而言完全没用，因此我们需要选择不同的特征来进行任务。方法有 ：尝试所有的可能性 ：算法本身决定使用和忽略哪些属性，构造决策树分类器算法 ：使用某种独立于数据挖掘任务的方法，在数据挖掘算法运行前进行特征选择，例如我们可以选择属性的集合，它的属性之间相关性应该尽可能的低。 ：通常并不枚举所有可能性来找出最佳子集。 这是特征子集的选择方式：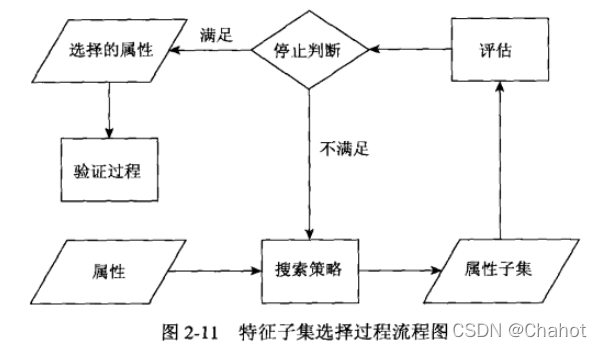 
特征创建：用原来的属性创建新的属性集，更有效的捕获数据集中的重要信息。 ：由原始数据创建新的特征集乘坐特征提取。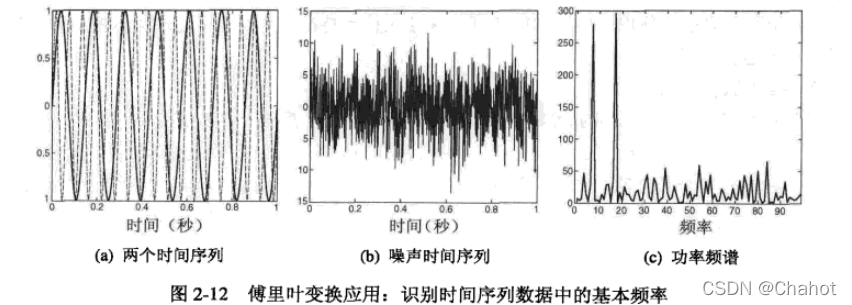 
:对时间序列数据，它们一般含有周期，噪音过多时并不容易检测，因此可以通过傅里叶变换转换为频率有关的新数据对象。 ：由一个或多个原特征中构造的新特性可能比原特征更有用。
离散化和二元化：一般用于分类。将连续的属性变为离散属性就是一个分类的过程。其中可能还会包含二元化。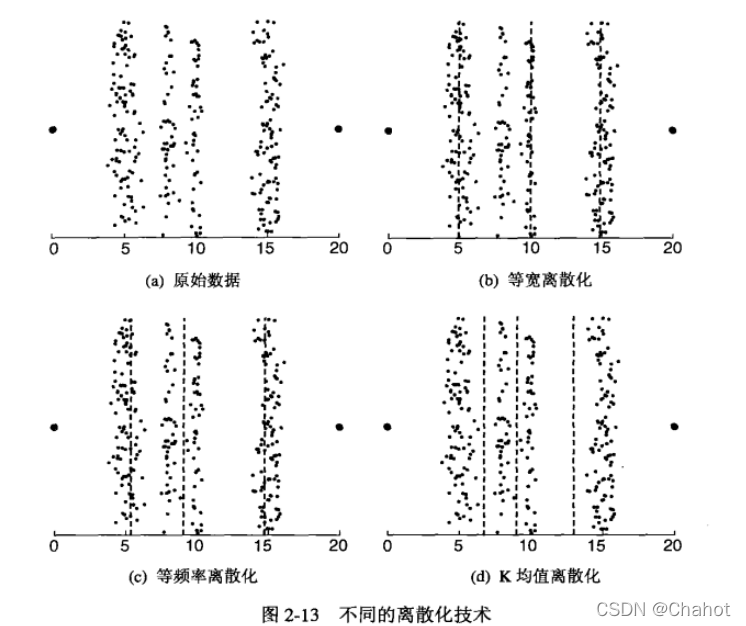 
这里有很多算法，不做详细介绍，总之离散化就是对数据的分类，便于更明确的赋予属性意义
变量变换：用于压缩数据的变量，如字节数的值域。传输10的指数次方的运算量是巨大的，但是对其指数的计算是轻松的。 标准化： 是整个值的集合 具有特定的性质。由于存在离群点，所以中位数的参考价值要大于均值，其次绝对标准差取代标准差。
相似度similarity：数值介于0-1，越接近1越相似 相异度dissimilarity：数值介于0~无穷大，越小越相似
某些相似度算法可能会局限相似度的数值，而某些体系的相似度可能不是0-1，因此我们需要转换它们。
如果是一个相似度为1-10的对象，相似度为6，则该式子的计算应该为6-1/10-1=5/9=0.5，这个公式也可以用来转换相异度
如果评价分为5个等级，分别得分01234，其中一个评价为2分的产品与一个评价为3分的产品，相异度为1. d=1-0/4-0=0.25 
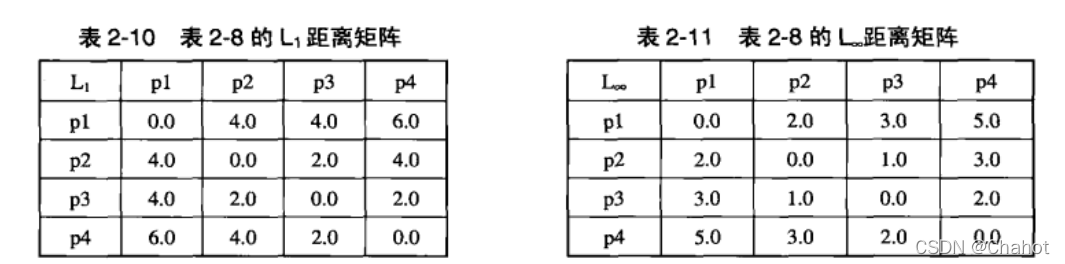
公式如上所示 为了更好的计算相异度d，定义了一个距离的概念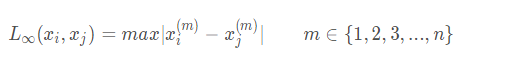 
其中n是维数，x和y是属性k的分量。用一个例题来表述： p1与p2的距离与p2与p1的距离是相等的，计算结果是根号8，约为1.4*2=2.8。其实就是两点对应同纬度标量的加减法 如此计算可以从表8得到表9. 
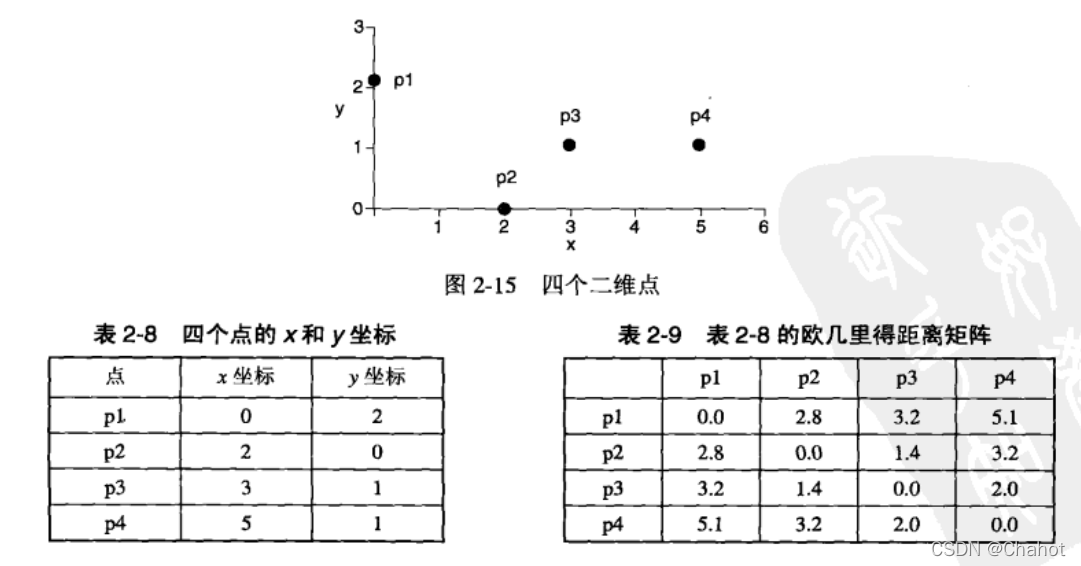然后是第二个定义公式： 
以p1,p2为例，计算为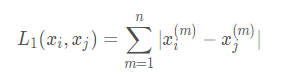 
L1:2+2=4，填入表8. L2：2.8；刚才计算过的距离 L∞：2-0=2
